1. 概念

本文科普一下高斯白噪声（white Gaussian noise, WGN）。

百度百科上解释为“高斯白噪声，幅度分布服从高斯分布，功率谱密度分布服从均匀分布”，听起来有些晦涩难懂，下面结合例子通俗而详细地介绍一下。

白噪声，如同白光一样，是所有颜色的光叠加而成，不同颜色的光本质区别是它们的频率各不相同（如红色光波长长而频率低，相应的，紫色光波长短而频率高）。白噪声在功率谱上（若以频率为横轴，信号幅度的平方为功率）趋近为常值，即噪声频率丰富，在整个频谱上都有成分，即从低频到高频，低频指的是信号不变或缓慢变化，高频指的是信号突变。

由傅里叶变换性质可知，时域有限，频域无限；频域有限，时域无限。那么频域无限的信号变换到时域上，对应于冲击函数的整数倍（由公式也可推得）。即说明在时间轴的某点上，噪声孤立，与其它点的噪声无关，也就是说，该点噪声幅值可以任意，不受前后点噪声幅值影响。简而言之，任意时刻出现的噪声幅值都是随机的（这句话实际上说的就是功率谱密度分布服从均与分布的意思，不同的是，前者从时域角度描述，而后者是从频域角度描述）。这里要指出功率谱密度（Power Spectral Density, PSD）的概念，它从频域角度出发，定义了信号的功率是如何随频率分布的，即以频率为横轴，功率为纵轴。

既然白噪声信号是“随机”的，那么反过来，什么叫做“相关”呢？顾名思义，相关就是某一时刻的噪声点不孤立，和其它时刻的噪声幅值有关。其实相关的情况有很多种，比如此时刻的噪声幅值比上一时刻的大，而下一时刻的噪声幅值比此时刻的还大，即信号的幅值在时间轴上按从小到大的顺序排列。除此之外，幅值从大到小，或幅值一大一小等都叫做“相关”，而非“随机”的。

解释完了“白噪声”，再来谈谈“高斯分布”。高斯分布，又名正态分布（normal distribution）。概率密度函数曲线的形状由两个参数决定：平均值和方差。简单来说，平均值决定曲线对称中线，方差决定曲线的胖瘦，即贴近中线的程度。概率密度定义了信号出现的频率是如何随着其幅值变化的，即以信号幅值为横轴，以出现的频率为纵轴。因此，从概率密度角度来说，高斯白噪声的幅度分布服从高斯分布。

描述了“白噪声”和“高斯噪声”两个含义，那么，回到文章开头的解释：高斯白噪声，幅度分布服从高斯分布，功率谱密度分布服从均匀分布。它的意义就很明确了，上半句是从空域（幅值）角度描述“高斯噪声”，而下半句是从频域角度描述“白噪声”。

2. 举例

下面以matlab程序演示，感性认识一下高斯白噪声。

2.1. 程序1（高斯白噪声）

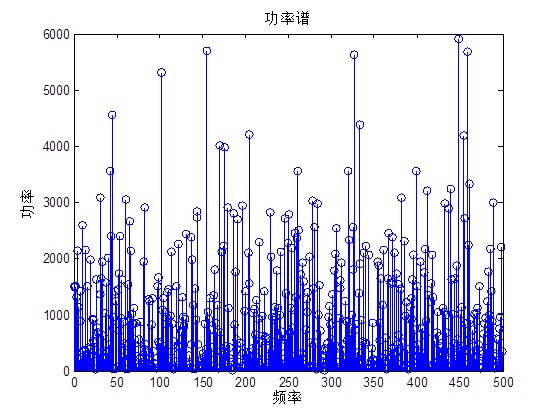
由上图可以看出，高斯白噪声的功率谱密度服从均匀分布。

若对噪声进行由小到大排序，则使其从随机噪声变为相关噪声，则功率谱密度就不再是均匀分布了。

2.2. 程序2（非高斯白噪声）

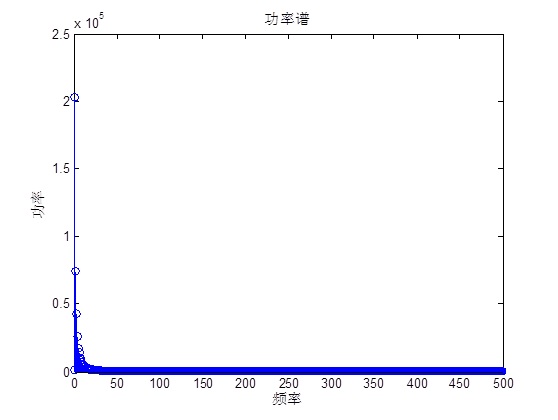
下面让我们从高斯白噪声的统计信息和幅值分布看一下它的特点。

2.3. 程序3（高斯白噪声）

高斯白噪声的标准差（standard deviation）可以改变。

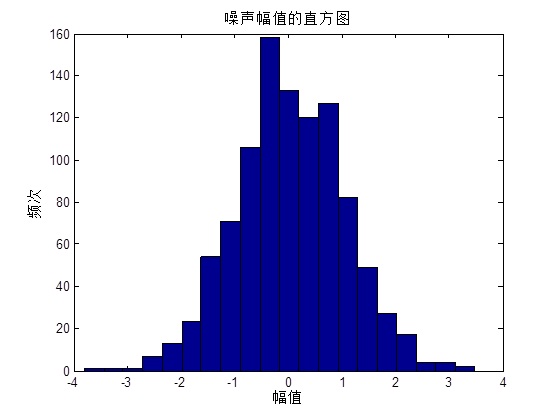
直方图的纵轴为频次，而概率密度的纵轴为频率，但是两者大致的分布曲线却是一样的，因此，这幅图解释了高斯白噪声的幅度分布服从高斯分布。

阅读延伸：

正态分布的函数（又称密度函数）为：

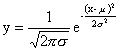                               (1)

式中π是圆周率3.14159...

e是自然对数的底2.71828…

x为随机变量取值一∞<x<∞

μ为理论的平均数

σ2为理论的方差

y为概率密度即正态分布上的纵坐标。

依上面的公式，当x＝μ时，上式可写作：

y＝，

当σ＝1时，＝0.3989在中央点的y最高，即y的最大值为0.3989。

正态分布的图形见下图1。

图1 正态分布的图形

正态曲线下的面积为1，由于它在平均数处左右对称，故过平均数点的垂线将正态曲线下的面积划分为相等的两部分，即，各为0.50。正态曲线下各对应的横坐标（即标准差）处与平均数之间的面积可用积分公式加以计算：

                      (5—3)

式中σ为标准差，，Z的大小随变量X的值而变。因正态曲线下每一横坐标所对应的面积与总面积（总面积为1）之比其值等于该部分面积值，故正态曲线下的每一面积可视为概率，即值为每一横坐标值（灭加减一定标准差）的随机变量出现的概率。

(五)正态分布是一族分布。它随随机变量的平均数，标准差的大小与单位不同而有不同的分布形态。如果平均数相同，标准差不同，这时标准差大的正态分布曲线形式低阔，如果标准差小，则正态曲线的形式高狭。

但所有的正态分布都可通过（或）容易地转换成标准正态分布。根据Z分数的性质（见第三章）亩知，标准正态分布的μ＝0，σ2 =1。标准正态分布通常写作N(0,1)正态分布。从正态分布的密度函数可知，正态分布的两个重要的参数是：平均数和标准差。而标准正态分布这两个参数分别为0与1。

标准正态分布的密度函数可写作：

由此其密度函数及面积（或概率）的计算可大大简化。目前各种统计书后面都列有标准正态分布的统计表，它可应用于一切正态分布形式、使用简便，已不再需要每次去进行繁复的计算了。